- Mazes For Programmers part 1, introduction
- Mazes For Programmers part 2, some basics
- Mazes For Programmers part 3, graphical UI
- Mazes For Programmers part 4, implementing the first two algorithms
- Mazes For Programmers part 5, Dijkstra’s algorithm
- Mazes For Programmers part 6, paths through the mazes
- Mazes For Programmers part 7, the Aldous-Broder algorithm, and when random is not very random
- Mazes For Programmers part 8, a random walk with Wilson’s algorithm
- Mazes For Programmers part 9, some statistics, and combining the Aldous-Broder and Wilson’s algorithms
- Mazes For Programmers part 10, improving the Aldous-Broder algorithm to remove short dead-ends
- Mazes For Programmers part 11, Ruby vs C# speed tests
- Source code on GitHub
Having implemented Dijkstra’s algorithm, the next bit of fun was to use it to find paths through the maze.
Although I had looked at his code in the book, I decided to have a go at writing my own method from scratch, rather than converting his code into C#. This is a better way to understand the algorithms, and saved me having to figure out some of the less obvious language Ruby features. The end result was actually very similar to his code, although I made use of Linq (yet again) to avoid a loop, making the code a little clearer…
public List<Cell> PathFrom(int row, int col) {
CellDistance start = Cells.FirstOrDefault(c => c.Cell.Row == row && c.Cell.Col == col);
if (start == null) {
throw new ArgumentException($"No such cell at ({row}, {col})");
}
List<Cell> path = new List<Cell> { start.Cell };
CellDistance current = start;
while (current.Cell != Root) {
CellDistance next = Cells.First(c => current.Cell.Links.Contains(c.Cell)
&& c.Distance == current.Distance - 1);
current = next;
path.Add(current.Cell);
}
return path;
}
I called my method PathFrom, as you specify where you want to go from, and it gives you a path from there to the root of the Distances object. He called his path_to, presumably because it gives you a path to the specified cell from the root. I guess this is a matter of taste.
The next task was to find the largest distance from the root. Again, Linq to the rescue, and I was able to convert this…
def max
max_distance = 0
max_cell = @root
@cells.each do |cell, distance|
if distance > max_distance
max_cell = cell
max_distance = distance
end
end
[max_cell, max_distance]
end
…into this…
public CellDistance Max =>
new CellDistance(_distances.Keys.Last(), _distances[_distances.Keys.Last()]);
Actually, I say “convert,” but it wasn’t really a conversion, I took one look at his code and decided to write my own. Recall that I added a CellDistance class to wrap the cell and distance together. I could have used tuples like he did, but as the two values are so closely coupled, I preferred to couple them.
For those of you who are trying to work out how this code finds the maximum distance, it’s worth remembering how Dijkstra’s algorithm actually works. Recall that we start with a root cell, which we mark as having distance zero, then pick all immediately linked cells, and mark them as having distance 1. We then pick all cells immediately linked to the ones with distance 1 and mark them with distance 2 and so on.
The end result of this is that we add cells to the distances collection in increasing order of distance. The end result is that the cell(s) with the highest distance go in last. Therefore, all we need to do is pick the very last cell added, safe in the knowledge that this has the highest distance in the maze.
Now this is all based on the fact that I know the items are stored in the order in which they were added, so I’m safe in taking the last one. If I didn’t know that (say we were using another algorithm for finding distances), then the following property would give the maximum, and does not rely on the order…
public CellDistance Max =>
Cells.Aggregate((i1, i2) => i1.Distance > i2.Distance ? i1 : i2);
This uses the vastly underrated Aggregate method to find the CellDistance instance with the maximum distance. Recall that the standard Max method would only return the actual distance, not the full CellDistance object, so we need to use Aggregate. Bearing in mind that many standard Linq methods (such as Sum, Max, etc) can be defined in terms of Aggregate, this shouldn’t really be any surprise.
What none of these methods account for is that there may be multiple cells with the same maximum distance. It wouldn’t be too hard to change the property to return all cells with that maximum distance, so you could look at them all. That’s something I would like to look at sometime.
Once I had this property, my code for finding the longest path through a maze looked pretty much like his.
In order to display the path (or any path), I added the following method to the window’s code-behind…
private void DrawPath(List<Cell> path, double hCellSize, double vCellSize) {
Cell start = path.First();
double prevX = start.Col * vCellSize + vCellSize / 2;
double prevY = start.Row * hCellSize + hCellSize / 2;
path.Skip(1).ForEach(c => {
double thisX = c.Col * vCellSize + vCellSize / 2;
double thisY = c.Row * hCellSize + hCellSize / 2;
DrawLine(prevX, prevY, thisX, thisY, _pathBrush);
prevX = thisX;
prevY = thisY;
});
}
This was a bit messier than I’d hoped, but not complex. I may come back and revisit it at some point, but as this sort of stuff is less interesting than the maze code, I’ll probably leave it as it works. The result looked like this…
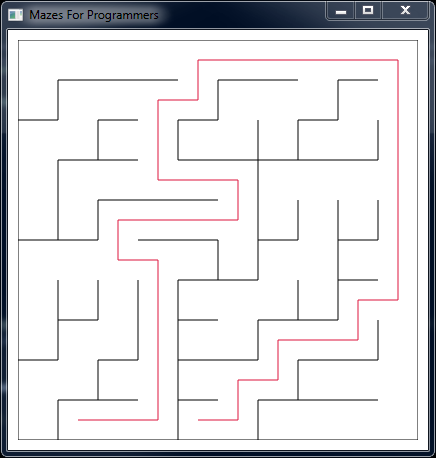

Be First to Comment