Mazes For Programmers part 11, Ruby vs C# speed tests

• Tweet
• Email

• Tweet
• Email

Following on from my experiments in timing the algorithms in part 9 of this series, I was curious as to why my code for Wilson’s algorithm took so much longer than the code for the Aldous-Broder algorithm.

Jamis Buck (the author of the book this is all based on) was foolish enough to leave his email address on his blog, inviting people like me to ask him questions! I asked if he had seen anything like this difference. Turns out he hadn’t actually tried timing them, so couldn’t comment.

This got me curious, so I pulled up his code, and started searching around to find out how to time code in Ruby. This turned out to be fairly simple (as it should), giving me the following…

require 'benchmark'

for i in 1..10
  s = Benchmark.realtime {
    maze = Grid.new(100, 100)
    AldousBroder.on(maze)
  }
  puts(s)
end

This gave me 10 numbers, which enabled me to calculate an average, as well as check on the variation (standard deviation for the statistical types). I forgot to mention in the earlier post, but I was intrigued to see that my implementation of Wilson’s algorithm was fairly consistent in its running speed, whereas my conversion of his code into C# led to a much wider variation in running speed…

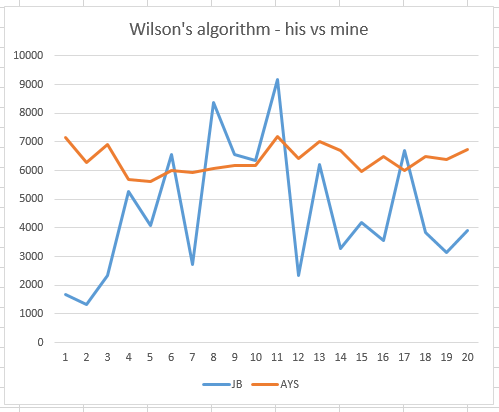
The orange line is my version, which is fairly steady around the 6-7s mark, whereas his version showed a much bigger variation.

I know a line graph isn’t strictly the right thing here, as the numbers aren’t in any sequence, but forgive me, I’m not a statistician!

Anyway, returning the previous point, I was now in a position to time his two Ruby implementations and compare them to mine…

All numbers are milliseconds, and the the ones for my C# code are the ones shown in the earlier blog post.

Interestingly enough, my code was faster than his for both algorithms, despite me not having had any thoughts for optimisation when I wrote it (although in fairness, presumably neither did he). Aldous-Broder runs fast enough that the differences aren’t really significant (although technically mine is about 26% faster than his), but Wilson’s showed a huge difference. Whilst my implementation was around 8 times slower than my Aldous-Broder code, his was around 31 times slower than his Aldous-Broder code.

Resisting the temptation to gloat over the apparent speed advantage I had using C# over Ruby, my conclusion is that it seems that Wilson’s is significantly slower that Aldous-Broder. Given that it appears to produce equally good mazes, I guess there’s no advantage to it.