- Mazes For Programmers part 1, introduction
- Mazes For Programmers part 2, some basics
- Mazes For Programmers part 3, graphical UI
- Mazes For Programmers part 4, implementing the first two algorithms
- Mazes For Programmers part 5, Dijkstra’s algorithm
- Mazes For Programmers part 6, paths through the mazes
- Mazes For Programmers part 7, the Aldous-Broder algorithm, and when random is not very random
- Mazes For Programmers part 8, a random walk with Wilson’s algorithm
- Mazes For Programmers part 9, some statistics, and combining the Aldous-Broder and Wilson’s algorithms
- Mazes For Programmers part 10, improving the Aldous-Broder algorithm to remove short dead-ends
- Mazes For Programmers part 11, Ruby vs C# speed tests
- Source code on GitHub
One of the things I like about this book is that he ends each chapter with ideas of things to try yourself. Copying someone else’s code isn’t that exciting, converting someone else’s code from one language to another (as I started off doing) is a bit better, but not much. Reading someone’s description of an algorithm and implementing it yourself is where the fun begins, but playing around with it afterwards is where you started wondering why you can’t get paid for doing this!
Having described Aldous-Broder and Wilson’s algorithms, he suggested combining them. Aldous-Broder starts off carving cells out quite quickly, but slows down towards the end as it tries to find the last few unvisited cells. By contrast, Wilson’s algorithm starts off slowly, as it takes a while for the random walk to find previously visited cells, but speeds up towards the end, as there aren’t many unvisited cells left to find. He suggested doing a combined algorithm that had the benefits of both.
Analysing Aldous-Broder
However, before doing so, I wanted some idea of how the two existing algorithms performed. This was easy to work out for Aldous-Broder, as you carve as you go along, so you always know how far you are through the algorithm. I decided to add some tracing to the code, so see how long it took to visit 10%, 20%, etc of the cells. As I was going to need to run this several times, to get an average, I wanted a way of returning the statistics to the calling code, but didn’t want to change the signature of the Create method, as that would have broken the code that used it.
I settled on a compromise, and added a static array to hold the data. I then needed to check every time I got 10% further through the number of cells, and log the number of iterations. The code ended up like this…
public static class AldousBroder {
public static int[] Iterations;
public static Maze Create(int rows, int cols) {
Iterations = new int[10];
int totalCells = rows * cols;
int tenPercent = totalCells / 10;
Maze maze = new Maze(rows, cols);
Random r = new Random((int)DateTime.Now.Ticks);
int unvisited = rows * cols - 1;
Cell current = maze.Cells.Rand(r);
int iterations = 0;
int currentPercent = tenPercent;
int n = 0;
while (unvisited > 0) {
if (totalCells - unvisited == currentPercent) {
currentPercent += tenPercent;
Iterations[n] = iterations;
n++;
}
Cell next = current.Neighbours.Rand(r);
if (next.Links.Count == 0) {
current.Link(next);
unvisited--;
}
current = next;
iterations++;
}
Iterations[n] = iterations;
return maze;
}
}
I’ve highlighted the extra code I added, which should be fairly self-explanatory. I didn’t commit this code, as I don’t want it long-term, so this is the only place you’ll see it.
Dumping the output from this into Excel showed a graph that looked as you would expect…
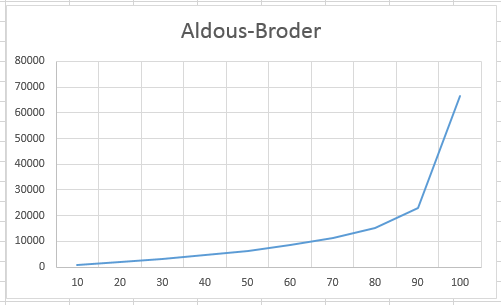
The numbers along the x-axis are the percentage, and the numbers up the y-axis are the iterations required to reach those percentages. As you can see, you get about 90% of the maze carved out in about 20,000 iterations (about 25% of the total time), with the remaining 10% of the cells taking up about the rest of the computation time.
Analysing Wilson’s
Tracing Wilson’s algorithm turned out to be a lot harder, as you only carve out when you reach a previously visited point, and that can be at any percentage through the execution. Also, as you do this many times, you end up dumping out a lot more numbers. After fiddling about with a static array, I gave up and used Debug.WriteLine to output the data…
public static Maze Create(int rows, int cols) {
int totalCells = rows * cols;
Maze maze = new Maze(rows, cols);
Random r = new Random((int)DateTime.Now.Ticks);
List<Cell> walk = new List<Cell>();
// Pick a random cell to mark as visited. This will be the end point of our first walk
Cell first = maze.Cells.Rand(r);
// Pick a starting cell for our first walk
Cell current = maze.Cells.Where(c => c.Row != first.Row && c.Col != first.Col).Rand(r);
walk.Add(maze.Cells.First(c => c.Row == current.Row && c.Col == current.Col));
int iterations = 0;
int n = 0;
while (maze.Cells.Any(c => !c.Links.Any())) {
Cell next = walk.Last().Neighbours.Rand(r);
if (next == first || next.Links.Any()) {
walk.Add(next);
// Carve cells along the current walk
walk.Zip(walk.Skip(1), (thisCell, nextCell) => (thisCell, nextCell))
.ForEach(c => c.thisCell.Link(c.nextCell));
if (n == 25 || n % 50 == 0) {
Debug.WriteLine($"{iterations}\t{maze.Cells.Count(c => c.Links.Any()) * 100 / totalCells}");
}
n++;
// If there are any unvisited cells, start a new walk from a random one
if (maze.Cells.Any(c => !c.Links.Any())) {
walk = new List<Cell> { maze.Cells.Where(c => !c.Links.Any()).Rand(r) };
}
} else if (walk.Contains(next)) {
// Snip off all cells after the last time we visited this cell
walk = walk.Take(walk.IndexOf(next) + 1).ToList();
} else {
walk.Add(next);
}
iterations++;
}
Debug.WriteLine($"{iterations}\t{maze.Cells.Count(c => c.Links.Any()) * 100 / totalCells}");
return maze;
}
I dumped out the data when the walk reached a previously visited cell, but only did this on the 25th time, and every 50th. This cut down the number of data points to a manageable level. The reason for the hard-coded 25 was that it didn’t seem to output much data near the beginning, so I added that one to get some early data as well.
Putting this into Excel showed the opposite behaviour from Aldous-Broder, again as expected…
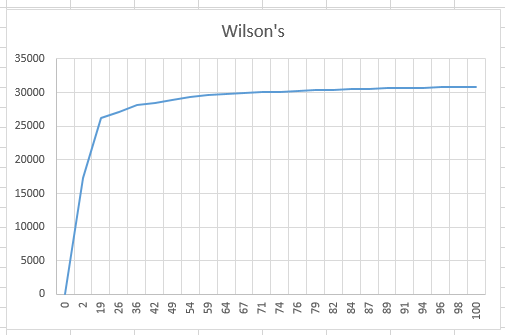
You see that this takes a lot of iterations to get the first 40% of the cells visited, but then a lot less iterations to find the rest.
Comparing all the algorithms so far
Running some timings on all of the algorithms so far have average times for producing 50×50 mazes…
| Algorithm | ms |
|---|---|
| BinaryTree | 5 |
| Sidewinder | 1 |
| Aldous-Broder | 51 |
| Wilson | 427 |
You can see how much faster the first two algorithms are, but at the (significant) cost of their biases. What surprised me was how much faster Aldous-Broder was than Wilson’s. Each one has its advantages and disadvantages, and I expected them to cancel each other out overall. However, unless my code is particularly poor for Wilson’s, or (less likely) particularly good for Aldous-Broder, the latter really does seem a quicker algorithm.
A combined Aldous-Broder and Wilson’s algorithm
This turned out to be a lot easier than I expected. I set a target percentage, and ran Aldous-Broder until I had visited that percentage of cells, then switched to Wilson’s. The only major change here was that I had to be a little more careful picking the very first cell, and the beginning of the first walk, as I didn’t have the previous advantage of an empty maze. However, this was merely a matter of filtering the cells to select only those without any links, and then picking random ones from those.
public static Maze Create(int rows, int cols) {
int abMaxPercentage = 80;
int totalCells = rows * cols;
int tenPercent = totalCells / 10;
Maze maze = new Maze(rows, cols);
Random r = new Random((int)DateTime.Now.Ticks);
int iterations = 0;
// Start off with Aldous-Broder. Run this until we have carved a specified percentage of cells
int unvisited = rows * cols - 1;
Cell current = maze.Cells.Rand(r);
int currentPercent = tenPercent;
int n = 0;
while (unvisited > 0 && currentPercent < abMaxPercentage) {
if (totalCells - unvisited == currentPercent) {
currentPercent += tenPercent;
n++;
}
Cell next = current.Neighbours.Rand(r);
if (next.Links.Count == 0) {
current.Link(next);
unvisited--;
}
current = next;
}
// Now switch to Wilson's
List<Cell> walk = new List<Cell>();
Cell first = maze.Cells.Where(c => !c.Links.Any()).Rand(r);
current = maze.Cells.Where(c => !c.Links.Any()).Rand(r);
walk.Add(maze.Cells.First(c => c.Row == current.Row && c.Col == current.Col));
while (maze.Cells.Any(c => !c.Links.Any())) {
Cell next = walk.Last().Neighbours.Rand(r);
if (next == first || next.Links.Any()) {
walk.Add(next);
walk.Zip(walk.Skip(1), (thisCell, nextCell) => (thisCell, nextCell))
.ForEach(c => c.thisCell.Link(c.nextCell));
if (n == 25 || n % 50 == 0) {
}
if (maze.Cells.Any(c => !c.Links.Any())) {
walk = new List<Cell> { maze.Cells.Where(c => !c.Links.Any()).Rand(r) };
}
} else if (walk.Contains(next)) {
walk = walk.Take(walk.IndexOf(next) + 1).ToList();
} else {
walk.Add(next);
}
}
return maze;
}
It is likely that with a bit of thought, I could have spiffed up this code up a lot, but I didn’t bother, mainly because the new algorithm didn’t seem to be particularly better. Running some timings on this gave an average time of 396ms to generate a 50×50 cell maze. This was faster than the plain Wilson’s algorithm, but but still a lot slower than the plain Aldous-Broder. Given that all three have the same lack of bias, there didn’t seem to be any point in refining this combined algorithm.
So, an interesting exercise, if a slightly disappointing conclusion. I was hoping that the combined algorithm would have beaten both of its parents.
Be First to Comment