I’ve just finished reading Humble Pi by Matt Parker for the second time. This was one of the most entertaining books I’ve read for a while. Mind you, considering I was reading The Plague by Albert Camus at the same time, that’s probably not saying much! That would have been grim reading at any time, but was even more so in the middle of the coronavirus lockdown.
One of the reasons I enjoyed it so much (Humble Pi, not The Plague, that didn’t contain any jokes at all) was that the author has the same weird sense of humour as I do. For example, the page numbers in the index are not integers like in a normal book, they are specified to five decimal places, where the decimal part indicates how far down the page the entry is to be found. The pages number downwards by the way, so the book starts on page 313, and ends on page zero. There is then what looks like a maths overflow, as the index starts on page 4,294,967,295 and decreases from there!
Anyway, starting from page 254, he begins a rant about the way people (ab)use Excel, and along the way, he digresses into telephone numbers…
For s start, just because something walks like a number and quacks like a number does not mean it is a number. Some things which look like numbers are not. Phone numbers are a perfect example: despite being made from digits, they are not actually numbers. When have you ever added two phone numbers together? Or found found the prime factors of a phone number? (Mine has eight, four distinct.)
Now as I said, I have a weird sense of humour, but that comment in brackets had me doubled over with laughter. Having ranted about how you don’t do maths with phone numbers, he admits that he did, and even sounds quite proud of the fact that four of his prime factors are distinct.
Well this got me thinking. I wonder what the prime factors of my phone number are? Spoiler: there are four, three of which are distinct, so my phone number os obviously more exclusive that Matt Parker’s!
Always on the lookout for ways to improve my coding skills, I decided to see if I could come up with a single Linq expression that would find the prime factors of my phone number (or yours, except that I don’t know what it is). No, there isn’t really any logical reason to do this, it just struck me as being an interesting exercise, and one that I think Matt Parker would approve of.
The first thing to do was generate a sequence of prime numbers. As this wasn’t really part of my exercise, I didn’t feel it was cheating too much to search around for someone else’s code for this bit. Somewhere in the Great Depths Of The Internet I found the following code (source long since forgotten, apologies to the original author) which generates a sequence of all the primes up to the number supplied…
List<int> GeneratePrimes(int n) => Enumerable.Range(2, n - 1).AsParallel() .Where(i => Enumerable.Range(1, (int)Math.Sqrt(i)).All(j => j == 1 || i % j != 0)) .OrderBy(p => p) .ToList();
This is actually pretty simple, it uses Enumerable.Range to generate the sequence 0, 1, 2, …, n, and then the Where clause filters out ones that are divisible by any number up to the square root of the current number. This isn’t necessarily the most efficient way to do it, but it’s fast enough for the purpose.
With that, it turned out to be surprisingly easy to find prime factors…
GeneratePrimes(target)
.Where(p => target % p == 0)
.Select(p => new {
Prime = p,
Exponent = Enumerable.Range(1, target / p)
.Where(n => target % Math.Pow(p, n) == 0)
.Last()
});
Line 1 generates all the primes up to and including the target number. We need to check all of them, as if you are amongst the privileged few who phone number is prime, then you’ll just end up with that as the one factor. Strictly speaking, as any factor other than the number itself has to be no greater than half of the target, I could have optimised code by only checking numbers up to a half. If I found any prime factors then I was done, if not, the number itself is prime. However, that would have led to less elegant code, so I didn’t go down that route, although as I type this, I think I might try it out!
Line 2 filters out all primes that are not factors of our target. Lines 3-8 then project the prime factors into an anonymous type that contains the prime, and the exponent of that prime. That latter part was done by generating a list of numbers up to target/p, which is the highest number of time the prime could possibly divide into the target, then picking the last one. Again, I’m sure that someone cleverer than me could find a more efficient way of doing this, but it worked.
Running this on 123456 gives output like this…
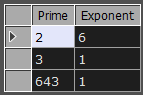
This says that the number 123456 is 2 to the power 6, multiplied by 3 and 643, each to the power 1.
At this stage, I was technically done, but I decided to see if I could print the factorisation more neatly. This sounded like a use for the woefully underrated Aggregate() method. I think this puts a lot of people off as it looks a bit scary when you first see it, but it’s extremely powerful.
Inserting the following line at the end of the expression did the trick…
.Aggregate("", (res, item) => res
+ item.Prime + (item.Exponent > 1 ? "^" + item.Exponent : "")
+ ".").TrimEnd('.')
The previous result now looked like this…
2^6.3.643
Given that I was doing this in LinqPad, I had to settle for displaying exponents in the form 2^6, and use a dot for a multiplication sign (as using “x” made it hard to read). However, I think this was pretty good.
As mentioned earlier, the point of my exercise was to produce a single Linq expression. This isn’t necessarily the best way to approach coding, especially when dealing with something that could potentially take some time. I did contemplate writing an imperative version of the same code to see how the speed compared, but never got around to it. Maybe one day. Maybe.

I was curious about how unique a ten digit number of eight prime factors (4 unique) is, dropping the leading zero. I reckon there are about 7 million numbers between 7000000000 and 8000000000… So quite a few.